Heat advection via constant pore water velocity is here added to heat exchange due to conduction and phase change. The analytical solution is obtained from the Kurylyk et al. (2014, AWR) paper based on a reassessment of solutions by Lunardini (1998, Proc. 7th. Conf. Permf.). Although not physically realistic (constant velocity independent of ice saturation) this solution can be used for benchmarking purposes: “Lack of fidelity to physical processes does not limit ability to serve as a benchmark”.
The paper Kurylyk et al. (2014, AWR) details several alternative analytical solutions, the suggested benchmark cases, and the SUTRA code runs to compare with these solutions. For more details, one may refer to “Analytical solutions for benchmarking cold regions subsurface water flow and energy transport models: One-dimensional soil thaw with conduction and advection” by B. Kurylyk, J. McKenzie, K. MacQuarrie, C. Voss in Advances in Water Resources 70 (2014) 172–184.
A presentation of the TH1 Case was made by Barret Kurylyk during the kick off meeting (Kurylyk).
Benchmark cases 2 and 3 recommended by Kurylyk et al. (2014) are included in the InterFrost project as two TH1 cases differing by the flow velocity considered: Velocities of 10 and 100 m/yr should be considered. These benchmarks are based on the following analytical solution:
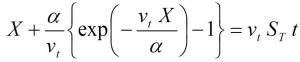where X is the depth to the thawing front, α is the thermal diffusivity, vt is the thermal plume velocity due to advection, t is time, and ST is the dimensionless Stefan number.
Benchmark 1 (Neumann solution) recommended by Kurylyk et al 2014 is an option to complement the Lunardini case provided in the InterFrost project as T1. For clarification purposes, it should be noted that the initial temperature (Ti) term in the Neumann solution is expressed as the number of degrees below 0°C (i.e. it is a positive number).
TH1 Test Case
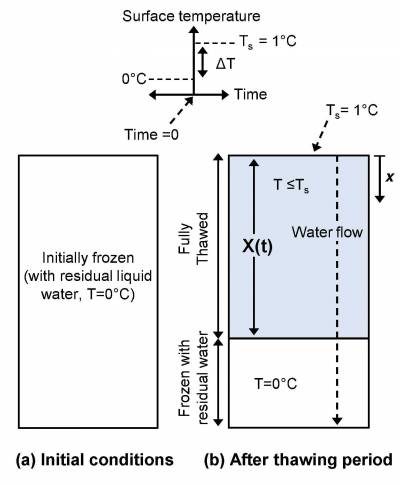
The initially uniform temperature is at 0°C. This condition simplifies the energy balance at the thawing front by ensuring that there is no thermal gradient (or conductive flux) below the thawing front. The specified surface temperature is above 0°C and hence induces thaw. The water is advected through the entire medium, but the divergence of the advective flux is zero below the thawing front due to the uniform thermal conditions.
Initial and boundary conditions:
The parameter table is accessible as docx file or as pdf file.
The analytical solution results selected by Kurylyk et al. (2014) for benchmarks are accessible here as an xls file.
Code developers are encouraged to email Barret Kurylyk (barret.kurylyk@ucalgary.ca) with any questions regarding the analytical solution or numerical model parameterization.
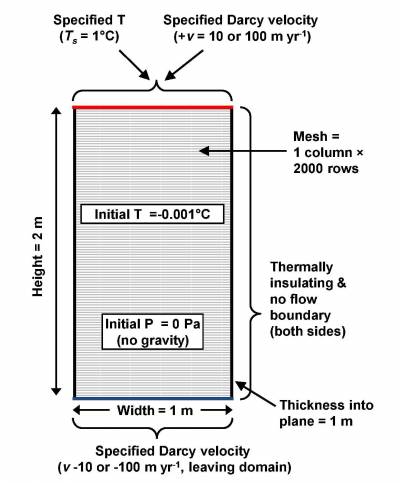
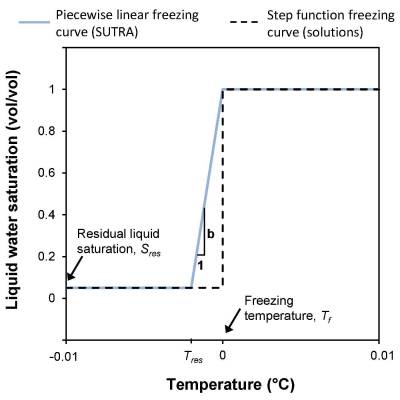
The approach used for SUTRA code is summed up in two figures from Kurylyk et al 2014 as a source of inspiration. They provide the simulated domain and the approach for the freezing curve function in order to approximate the step function with a linear curve:
