Case T1
Test Case T1 is an initial step towards the full set of coupled equations.It is limited to the heat transfer equation solely with conduction and phase change.
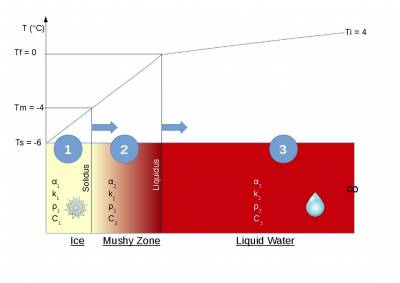
The T1 test case uses the existing analytical solutions. Several analytical solutions to the conduction problem with phase change exist: the Stefan solution, the solution by Lunardini, the Osterkamp solution. They all correspond to a 1D semi-infinite domain and an initial step of temperature at the boundary for an initially constant temperature domain. Following [McKenzie et al 2007] we suggest the Lunardini solution which, contrary to the Stefan solution (ice/water bar with phase change at 0°C) takes a range of temperature variation for the phase change. This configuration fits better to most models relying on finite element, finite volume or finite difference schemes (smooth interface) provided equivalent properties of the 3 zones are directly implemented (Ice, mushy zone, liquid water). The Stefan solution would be more appropriate for codes based on moving interfaces (sharp interface).
The 3-zone model (ice, mushy zone, liquid water) is illustrated below with a schematic temperature profile. The phase change domain is here the [-4°C; 0°C] range:
Parameters
The parameter values are provided as excel files for the Lunardini system and for the system of equations provided above (parameters.ods).
Performance measures
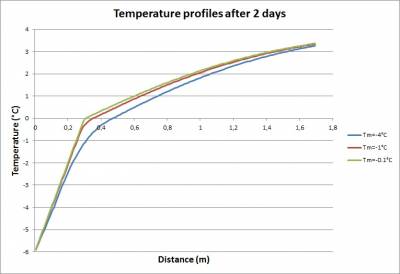
Performance measures are the temperature profiles simulated for a time equal to 2 days. Three values for the lower temperature of the phase change temperature range are considered: -4°C, -1°C, -0.1°C. For the sake of comparizon, the Lunardini analytical curves are plot in the figure below and provided as excel file. For the teams that would like to compare the results at 1 day and 3 days as well (optional), these curves are also provided in the excel files corresponding to the associated analytical curves (for temperature range [-0.1°C;0°C]:lunardini_tm_-0.1.ods, for [-1°C;0°C]: lunardini_tm_-1.0.ods, for [-4°C;0°C]: lunardini_tm_-4.0.ods).